Machine Learning - Linear Regression

이번 포스팅에서는 선형적 추정을 해볼 것이다. 예를 들어 우리는 집의 크기와 그 집들에 대한 가격에 대한 dataset이 있다고 해보자. 이런 경우, 집의 크기를 x, 가격을 y라 하면 우리는 input x에 대한 output y를 추정하는 함수를 구할 수 있을 것이다. 이런 추정을 하기 이전에 용어 정리부터 우선하자.
x(i) : i번째 input 변수
y(i) : i번째 output
cost function : 우리가 가정한 함수가 얼마나 정확한지 판단하는 함수. 모든 data들에 대해 평균적인 차이를 통해 얼마나 정확한지 판단한다. 아래와 같은 함수 형태로 쓸 수 있다.

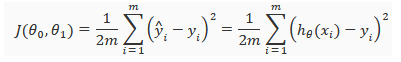
이제 우리가 해야할 것은 우리가 예측한 함수가 cost function이 최대한 낮게 나오도록 예측하는 것이다. 이때 사용할 수 있는 방법이 2가지가 있다. 하나는 Gradient Descent고 다른 하나는 Normal Equation이다.

Gradien Descent

Gradient Descent는 하나의 지점에서 시작한 뒤 그 주변을 둘러본 뒤 가장 가파른 방향으로 내려간다고 생각하면 된다. 이런 식을 반복하다보면 최저점은 아니여도 어느 수렴하는 한 지점까지 내려가게 된다.

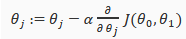
위의 식을 수렴할 때 까지 반복하면 된다. 이를 계속 반복하면서 극소점까지 내려가는 것이다. 위의 식을 보면 알파가 있는데 이는 얼마나 큰 비율로 내려가는지를 정하면 된다고 생각하면 된다. 알파값이 너무 큰 경우에는 수렴하지 않고 오히려 발산할 수 있어 문제가 발생할 수 있고 만약 알파값이 너무 작다면 극소점까지 도달하는 시간이 너무 오래 걸릴 것이다.

Normal Equation

Normal Equation은 주어진 식을 통해 바로 cost function이 최소가 되게 하는 값을 찾는 것이다.

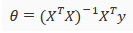
이 방식을 쓴다면 여러번 반복할 필요도 없다. 매우 좋아보이지만 이 방법에도 문제는 존재한다. 만약 각각의 case들에 대해 영향을 주는 features들이 너무 많다면 위의 식에서 X의 size가 매우 커지게 되고 이럴 경우 Matrices의 계산이 너무 느려지게 되어 이럴 경우에는 Gradient Descent를 통해 값을 찾아가는 것이 더 빠르다.